El número e=2,7182818284……………………………………………………………………………. es un número real, irracional, debido a que sus cifras decimales son infinitas y no tienen periodicidad.
Éste nuevo número e, se le suele llamar el número de Euler, en honor a Leonhard Euler (1707-1783) que descubrió muchas propiedades de éste número.
- Fue el primero en usar el símbolo e.
- Éste número, también es muy importante por ser la base de las funciones exponenciales (f(x)=e x ).
- Se ha dicho también, que Euler llamó en su día a éste número e, por significar exponencial o bien por ser la primera letra de su nombre.
No obstante, el número fue introducido por el matemático Escocés John Napier, que lo utilizó en el año 1600 aproximadamente para introducir los logaritmos Naturales o logaritmos Neperianos.
El número e es la base de los logaritmos Naturales o Neperianos.
- «e» es considerado el número por excelencia del CÁLCULO.
- «π» lo es de la TRIGONOMETRÍA.
- «i» el número del ANÁLISIS COMPLEJO.
- «Φ»de la divina proporción, aplicada al ARTE Y LA ARQUITECTURA.
El número e es irracional, al igual que el número Π y Φ; por ser decimal infinito no periódico.
También al igual que Π y Φ, el número «e» es un número trascendente.
CÁLCULO DEL VALOR DE «e»
si le damos valores , podemos observar su crecimiento, cada vez menor y que se aproxima al valor de «e».
A medida que vamos aumentando el número vemos que el resultado cada vez crece menos, hasta observar que prácticamente no crece nada.
El resultado es el número «e».
- El valor de «e» también es la suma siguiente, que se obtiene a partir de la formula de Taylor.

«!» significa «factorial» y se calcula multiplicando el número por sus sucesivos descendientes, hasta a unidad. 4!=4·3·2·1.
- El número “e” además de resolver los resultados de los límites de la indeterminación “ 1 elevado a infinito” aparece en otras fórmulas como la del interés compuesto continuo:

- El número «e» tiene un papel importante relacionado con los números complejos
- El caso especial con x = π es conocido como «IDENTIDAD DE EULER»
 de lo que se deduce que:
de lo que se deduce que: 
- Además, utilizando las leyes de la exponencial, se obtiene:
 que es la FÓRMULA DE MOIVRE.
que es la FÓRMULA DE MOIVRE.
APLICACIONES DE «e» A LA VIDA REAL
El número «e», los logaritmos neperianos y la función exponencial, tienen múltiples aplicaciones.
 En todas las ramas de la ciencia, la economía, en el crecimiento o decrecimiento de una determinada colonia de bacterias, etc.
En todas las ramas de la ciencia, la economía, en el crecimiento o decrecimiento de una determinada colonia de bacterias, etc.
- Cuando vemos un cable pendiente de dos cables, o una cadena sujeta por los extremos, su curvatura corresponde a la función:
 Napier
Napier
- Para determinar de una manera aproximada la antigüedad de un objeto que está formado por materia orgánica se mide la cantidad de carbono 14 que contiene. Los seres vivos tienen una cantidad de carbono 14 constante.
Cuando un ser vivo muere esta cantidad se va desintegrando. La función que regula la desintegración se determina con la siguiente fórmula: Q es la cantidad de carbono 14 final, Qo es la cantidad de carbono 14 inicial, t es el tiempo.
Q es la cantidad de carbono 14 final, Qo es la cantidad de carbono 14 inicial, t es el tiempo. - Absorción de los rayos X por la materia. Ley de Bragg-Pierce:
 I es la intensidad final del rayo después de atravesar el cuerpo, Io es la intensidad inicial de los rayos X, m es el coeficiente de absorción, x es el grueso del cuerpo.
I es la intensidad final del rayo después de atravesar el cuerpo, Io es la intensidad inicial de los rayos X, m es el coeficiente de absorción, x es el grueso del cuerpo. - Una de las numerosas aplicaciones en biología del número «e» es el crecimiento exponencial. Este tipo de crecimiento surge cuando no hay factores que limiten el crecimiento. Pueden experimentar un crecimiento exponencial las especies pioneras que llegan, por ejemplo, a zonas despobladas como una superficie boscosa en recuperación después de un incendio.
Para este tipo de crecimiento se aplica la siguiente fórmula:
N es la cantidad de población, No es la población inicial y «t» el tiempo.



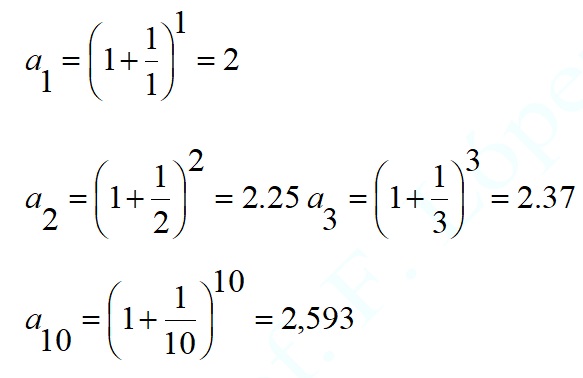





3 comentarios