Proyecciones y perspectivas-Evolución y aplicaciones

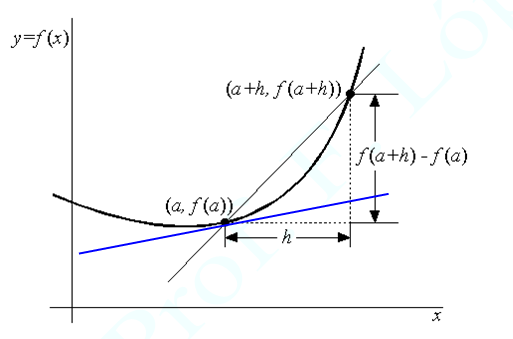
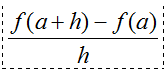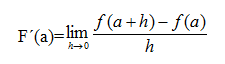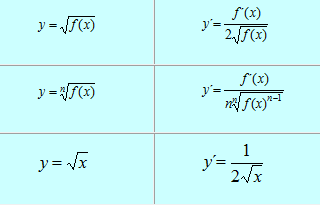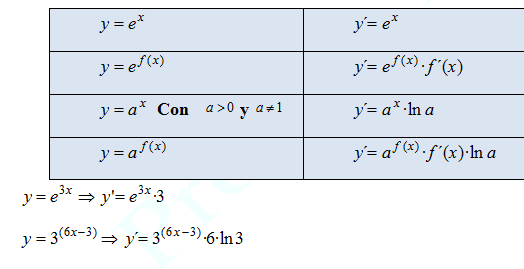Las proyecciones y la perspectiva tienen aplicaciones en la arquitectura y en el arte en general, desde los tiempos de la antigua Roma hasta la actualidad.

Representar los objetos tridimensionales en un plano. ¿Qué ley matemática es la que permite saber si la representación es “fiel”?

Proyección

Proceso de proyectar o representar un objeto tridimensional en un plano o superficie bidimensional.

La proyección gráfica es una técnica de dibujo empleada para representar un objeto en una superficie. La figura se obtiene utilizando líneas auxiliares proyectantes que, partiendo de un punto denominado foco, reflejan dicho objeto en un plano, a modo de sombra.

Los elementos principales de la proyección son:

• El punto de vista o foco de proyección.
• El punto que se desea proyectar.
• El punto proyectado.
• La línea proyectante.
• Y el plano sobre el que se proyecta, que recibe diferentes denominaciones como plano de proyección, plano de cuadro o plano imagen. 

PROYECTAR SOBRE UNA RECTA en el plano

Observamos primero la proyección de un punto sobre una recta y la de un segmento sobre un recta.

PROYECTAR SOBRE UNA RECTA EN EL ESPACIO

Igual que en el plano, primero la proyección de un punto y segundo la de un segmento.

PROYECCIÓN DE UN SEGMENTO EN UN PLANO Y LA DE UN PARALELEPÍPEDO EN UN PLANO DENTRO DEL ESPACIO

PRESPECTIVA

Es la proyección cónica desde un punto. La perspectiva se refiere a las técnicas utilizadas para representar la profundidad y la tridimensionalidad en una superficie bidimensional, como un lienzo o una hoja de papel. Esto implica el uso de líneas convergentes y puntos de fuga para crear la ilusión de distancia y espacio en una imagen. La perspectiva puede ser lineal, atmosférica u otros tipos según las reglas y principios utilizados.

La geometría proyectiva describe lo que vemos.
Las paralelas no se cortan, pero las vemos cortarse:

Proyecciones en rectas paralelas

PRESPECTIVA FRONTAL

La perspectiva frontal es un tipo de representación visual en el que un objeto o una escena se muestra de manera directa, como si se estuviera observando de frente. En la perspectiva frontal, los objetos se representan con sus dimensiones y formas tal como se ven desde una posición frontal sin ningún tipo de distorsión o inclinación.

Ls líneas paralelas que son perpendiculares al plano de visión (el plano imaginario que pasa por el ojo del observador) se representan como líneas paralelas en la imagen. Además, los objetos que están más cerca aparecen más grandes que los que están más lejos.

Se utiliza en dibujos técnicos, planos arquitectónicos, ilustraciones y representaciones gráficas donde se busca una representación precisa y fiel de los objetos desde una vista frontal. También es utilizado en fotografía y en diseño gráfico para mostrar objetos y elementos de manera clara y directa, sin ningún tipo de distorsión perspectiva que podría surgir en otros ángulos de visualización.

La perspectiva frontal es una representación visual en la que los objetos se muestran directamente desde una vista frontal, sin inclinaciones ni distorsiones, y con las líneas paralelas conservando su paralelismo en la imagen.

PRESPECTIVA OBLICUA

La perspectiva oblicua es un tipo de representación visual en el que los objetos y las escenas se muestran con una ligera inclinación o desviación con respecto al plano de visión. A diferencia de la perspectiva frontal, en la perspectiva oblicua los objetos no se presentan de manera completamente perpendicular al observador, sino que están ligeramente inclinados.

En la perspectiva oblicua, las líneas paralelas que son perpendiculares al plano de visión ya no se representan como líneas paralelas en la imagen, sino que se muestran con una ligera convergencia. Además, los objetos que están más cerca todavía aparecen más grandes que los que están más lejos, pero esta diferencia de tamaño puede ser menos pronunciada en comparación con la perspectiva frontal.

La perspectiva oblicua se utiliza a menudo en ilustraciones, cómics, animaciones y diseño gráfico para crear una sensación de profundidad y volumen. Al inclinar los objetos ligeramente, se logra una representación más dinámica y tridimensional. También se puede emplear en dibujos arquitectónicos y representaciones técnicas cuando se desea mostrar una vista que no es completamente frontal pero tampoco tan inclinada como en la perspectiva en profundidad.

“Virgen entronizada con dos ángeles” 1485-1490

Evolución de la perspectiva

Las primeras muestras están en la Antigua Roma, por intuición.

Mural pompeyano del siglo II dC. Tiene algún punto de fuga, pero no es una perspectiva completa.

En la época Medieval se trabaja en varios planos.

Jesús ante Caifás (1305) perspectiva inconsistente todavía.

Gentile di Fabriano: La Presentación en el templo (1423).

Van Eyck (1390 – 1441): todavía no hay dominio completo de la perspectiva. La Madonna del Canónigo van der Paele.

En  el siglo XIV se avanza un poco más- Pinturas de Giotto.

En  el siglo XV se avanza un poco más.

En  el siglo XV, Masolino da Panicale ya hace puntos de fuga en algún cuadro.

En  el siglo XV  nace la geometría proyectiva. Ejemplos de Masolino da Panicale.

RAFAEL-LA ESCUELA DE ATENAS

LA ÚLTIMA CENA DE LEONARDO DA VINCI

PINTURAS DE Julian Beever-1959.

BIBLIOTECA DE EL ESCORIAL Y PALACIO DE FONTAINEBLEAU

PRESPECTIVA SEGÚN DURERO

Puntos de vista desde lo alto

Puntos de vista medios

Puntos de vista bajos y muy bajo

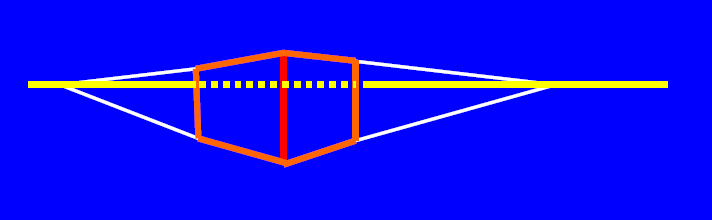
Las flechas indican el punto de mira o foco

Las técnicas

Velo de Alberti

Durero

Experimentos de Bruneleschi

Primero: Se trata de ver que un cuadro reproduce fielmente la realidad: se pinta un cuadro, se hace un pequeño agujero, se coloca un espejo delante, de modo que se vea el cuadro, y se retira el espejo: lo que se ve debe ser lo mismo que se veía en el cuadro.

Segundo: Quería obtener una vista del Palacio de la Señoría de modo que se vieran las dos fachadas.

Cámara oscura

Es una cámara fotográfica compuesta por una cámara oscura sin lente. Se emplearon desde mediados del XIX,
y se usan para fotografía artística. Tienen un orificio muy pequeño y en el fondo se coloca película que impresiona la luz.

• Tiene profundidad de campo infinita, aunque es muy poco luminosa.

DERIVADAS-DEFINICIÓN-FÓRMULAS-EJEMPLOS

Descartes, Newton y Leibniz favorecieron el desarrollo de la derivada, aunque el concepto del finito y el infinito lo trata Galileo al comparar los números y sus cuadrados.

DEFINICIÓN DE DERIVADA

La derivada es un concepto fundamental en cálculo y análisis matemático. Se refiere a la tasa de cambio instantánea de una función en un punto específico. En otras palabras, la derivada mide cómo cambia el valor de una función en respuesta a cambios infinitesimales en su variable independiente.

Es la pendiente de la recta tangente a la curva en un punto. La pendiente es la tangente del ángulo que forma la “recta tangente” con el eje de abscisas.

COCIENTE DE NEWTON O COCIENTE INCREMENTAL

Matemáticamente, la derivada de una función f(x) respecto a x, denotada comúnmente por f ‘(x) o dx/df​, se define como el límite cuando la variable de cambio (ℎ) tiende a cero de la razón de cambio promedio en un intervalo pequeño:

Es el cociente entre lo que aumenta la función y lo que aumenta la variable.

Esta expresión representa la pendiente de la recta tangente a la curva de la función en el punto x.

La derivada proporciona información sobre la rapidez con la que la función está creciendo o disminuyendo en un punto dado.

Se conoce como cociente de Newton o cociente incremental, pero también es la pendiente de la cuerda que pasa por A = (a, f(a)) y B= (a+h, f (a+h))

Si h tiende a cero el punto B se acerca al punto A y la recta cuerda se transforma en recta tangente, su pendiente es la derivada en un punto.

Se conoce como cociente diferencial o límite del cociente incremental.

Newton observó  que una función curva no crece en la misma proporción que la variable. Compara el crecimiento de la curva con la pendiente de la cuerda en un cierto intervalo. A esto le conocemos actualmente como cociente incremental o cociente de Newton, también en economía tasa de variación.

Su  método lleva  fácilmente  al cálculo de la pendiente de la recta tangente en un punto, pero por acuerdo entre Inglaterra y Alemania, esto se atribuye a Leibniz.

 En 1665  introdujo el concepto de fluxión, que para él era la velocidad con la que una variable «fluye» (varía) con el tiempo.

Leibniz descubrió y comenzó a desarrollar el cálculo diferencial en 1675. Fue el primero en publicar los mismos resultados que Newton descubriera 10 años antes. En su investigación conservó un carácter geométrico y trató a la derivada como el límite de  un cociente incremental y no como una velocidad. A él debemos el concepto de derivada o pendiente de la recta tangente a una curva en un punto.

Ejemplo

Supongamos que una pelota sigue la gráfica:

Como es un ejercicio que representa a un hecho real sería normal que solo se considere que x varía de x=0 a x=6.

Supongamos un intervalo:

Si resto 8-5=3 es lo que aumenta la variable, es decir f(x).

Si resto 2-1 es lo que aumenta la variable x.

Si divido los dos incrementos tengo lo que varía la función en ese intervalo

 que nos indicaría la velocidad media en el intervalo de tiempo que pasa de x=1 a x=2.

Pero como la función es una curva ese crecimiento varía en cada punto y también la velocidad.

Entonces surge la derivada como el incremento puntual de la función que nos mide la velocidad en cada punto.

Esto indica que la velocidad que lleva si x=2 es 10metros/seg.

Si esto lo tenemos que hacer en cada punto sería muy complicado, entonces lo que debemos hacer es calcular la derivada en cada punto, es decir:

A esto le llamamos función derivada.

Las fórmulas de las derivadas se demuestran con la definición y permiten calcular las pendientes con más facilidad.

En este caso f´(x)=-2x+6  y si calculamos f´(2)=2, lo mismo de antes, pero ahora podemos sustituir cualquier punto y saber la velocidad en cada momento.

• Calcular la función derivada de F(x) = 1/x con la definición. Calcular la derivada en el punto x=2

Ahora lo hacemos con x=2

Si queremos hacer la derivada con esta fórmula para cada función en cada punto sería largo y complicado, por ello hemos demostrado en general las fórmulas de cada función y las aplicamos para obtener la función derivada.

Supongamos una función y = f (x). Si en el punto de la curva (a, f (a)) trazamos una recta tangente, la pendiente de dicha recta tangente es la derivada de la función en el punto. La derivada varía si varía el punto. La función derivada representa a todas las pendientes en todos los puntos

Cada función tiene una función derivada, se puede hallar con la definición o con la tabla de las fórmulas, que se demuestran con la definición.

• Demostrar la derivada de y= x²

Lo que demuestra que en un punto x=2 la pendiente de la recta tangente es f´(2)=2·2=4

Si tenemos que hacer la pendiente en cada punto debemos tener la función derivada, y para ello tenemos la tabla de fórmulas de cada función que permite derivar todo tipo de funciones.

DERIVADA DE LA FUNCIÓN POTENCIA

La función potencia siempre tiene la variable en la base y el exponente es un número.

El exponente pasa a multiplicar a la función, y la función queda elevada a un grado menos.

 DERIVADA DE UNA CONSTANTE POR UNA FUNCIÓN

El exponente multiplica a la función, que ahora tiene un coeficiente que también queda multiplicado, y la función vuelve a quedar elevada el exponente menos.

DERIVADA DE UNA SUMA DE FUNCIONES

DERIVADA DE UNA CONSTANTE

 La derivada de una constante es cero.

DERIVADA DE UN PRODUCTO DE FUNCIONES

DERIVADA DE UN COCIENTE

DERIVADA DE UNA RAÍZ

DERIVADA DE UNA FUNCIÓN LOGARÍTMICA

 Siempre que en una derivada haya logaritmos, primero aplicamos sus propiedades y después derivamos, para simplificar la expresión.

PROPIEDADES DE LOS LOGARITMOS

Antes de derivar miro si se pueden aplicar las propiedades de los logaritmos, es más fácil y se simplifica mejor.

 DERIVADA DE UNA FUNCIÓN EXPONENCIAL

  DERIVADAS DE FUNCIONES TRIGONOMÉTRICAS

DEMOSTRACIÓN DE LA DERIVADA DEL ARCOSECANTE

DEMOSTRAR LA DERIVADA DEL  ARCOCOSECANTE

DEMOSTRACIÓN DE LA DERIVADA DEL ARCOCOTANGENTE

DEMOSTRACIÓN DE LA DERIVADA DEL ARCOTANGENTE

DERIVADA DE UNA FUNCIÓN ELEVADA A OTRA FUNCIÓN

EJERCICIOS RESUELTOS DE DERIVADAS

EJERCICIOS DE DERIVADAS PARA REPASAR

Prof: F. López- D. Legal: M-007076/2009

Función de variable normal

La distribución normal fue introducida por primera vez por Abraham de Moivre en 1733 como límite de una distribución binomial. Posteriormente, Carl Friedrich Gauss, en su estudio de los errores de medida de datos de observaciones astronómicas, indicó la expresión de la función de densidad de la distribución normal. Por ello esta distribución se conoce también con el nombre de “curva o campana de Gauss”.

Veremos como lo binomial se pasa a normal, cuando n es muy grande y a medida que es mayor el error que se comete al cambiar a normal es menor.

Distribución normal

En la vida real, muchos experimentos tienen una gráfica en forma de campana, se consideran “NORMALES”. Las áreas que encierran sus gráficas debajo de la curva se relacionan con la probabilidad, pero estas integrales no es necesario hacerlas, porque sus áreas están recogidas en la tabla normal de Gauss

La función de densidad recibe el nombre de curva normal o campana de Gauss.

Propiedades de la función normal

Ver tabla al final

Problemas de distribución normal

Los que entran tienen más nota que los que no entran, eso indica que el porcentaje está a la derecha, pero no se puede buscar en la tabla, por eso busco el simétrico de la derecha y luego cambio de signo.

Como el 70% está a la derecha, pasa lo mismo que en el problema anterior, busco el 0,7000 y luego por simetría el valor es negativo.

Problemas binomiales que pasamos a normales

Problemas normales

tabla normalDescarga

TABLA DE DERIVADAS CON EJEMPLOS

En este apartado os presento una tabla de derivadas con ejemplos de cada tipo. Luego en otros apartados hay mas ejercicios de derivadas.

 

Prof. F. López- D. Legal: M-007074/2009

Tabla de derivadas e integrales

Una de las herramientas más útiles para cualquier estudiante de bachillerato, es disponer de una tabla de derivadas y otra de integrales.

Tabla de derivadas con ejemplos

Tabla de derivadas simplificadaDescarga

Tabla de integrales con ejemplos

Tabla de integralesDescarga

Tipos de integrales

Tipos de integralesDescarga

Simetrías, tipos y aplicaciones en distintos ámbitos

Las simetrías son propiedades gfeométricas que están presentes en la naturaleza, en la arquitectura, el arte, las tecnologías, el diseño…

Vamos a definir las simetrías y sus tipos

Tipos de simetrías

Aplicaciones de las simetrías

Ya hemos visto logotipos con simetrías, también en las plantas de forma natural, en los animales y como aplicación decorativa en arquitectura y pintura.

Progresiones aritméticas-Fórmula general-Suma de términos y ejemplos

1.  LAS PROGRESIONES

Son un tipo especial de sucesiones (números ordenados) que tienen los términos relacionados entre si.

Hay dos tipos de progresiones:

• Aritméticas.

• Geométricas.

En este apartado, vamos a tratar las progresiones aritméticas.

2.  PROGRESIONES ARITMÉTICAS

Cada término se diferencia con el anterior en un valor constante, llamado diferencia.

• Primer término = a₁
• Segundo término = a₂= a₁+d
• Tercer término  = a₃=a₂+d= a₁+2d
• Término general  =a_n =  a₁  + (n-1)·d

Ejemplos:

1. Si el primer término es a₁ = 1, y la diferencia es d= 3, el término general es: a_n= 1+(n-1)·3=3n-2
2. Como me porto bien, mis padres deciden que la primera semana del año me dan una paga de 10 euros y cada semana me dan 2 más . ¿Cuánto me pagan la última semana? a₁₀ = 10+(52-1)·2=10+510=520euros
3. Si a₁=3 y d=-4, calcular a_n: a_n=3+(n-1)·(-4)=-4n+7

3.  SUMA DE TÉRMINOS DE UNA POGRESIÓN ARITMÉTICA

En el problema que calculo la paga que me dan en el último mes del año, nos podemos preguntar cuánto dinero me tienen que dar mis padres al final del año, y tengo dos opciones o calcular lo que cobro todas las semanas y sumarlo todo o aplicar alguna fórmula.

Si nos planteamos cuanto suman los primeros 60 números, observamos que forman una progresión aritmética de diferencia d=1 y el primer término también 1

Todas las sucesiones aritméticas verifica que si sumamos términos equidistantes del centro suman lo mismo.

Por tanto, tenemos 30 sumas iguales a 61. Esto lo observó Gauss con 9 años. y dedujo que para sumar los primeros 60 números, basta multiplicar 61 por 30=1830.

Acabamos de observar que hay una fórmula para sumar términos de una progresión aritmética: Primer término más el último, por el número de términos entre 2.

S_n=(a₁+a_n)·(n/2)

Calcular la suma de la progresión: 7, 10, 13, 16, 19…    en donde observo que d=3.

1. Calcular el término general.
2. El término 100.
3. La suma de los 6 primeros.

a_n=7+(n-1)·3=3n+4

a₁₀₀=7+(99)·3=304

S₆=(a₁+a₆)·(n/2)=(7+(3·6+4))(6/2)=(7+22)(3)=87

Interpolar en una progresión aritmética

Entre 18 y 46 interpolar un término de forma que resulte una progresión aritmética.

18+x es el número que buscamos.

18+x +x tiene que resultar igual a 46

2x=46-18

x=14

El número que buscamos es 18+14=32

Ejemplo de suma de t´´erminos en progresión aritmética:

Al comienzo del año Juan decide ahorrar para comprarse la play. En Enero, mete en su hucha 10€ y cada mes introduce la misma cantidad, 1€ más.

¿Cuánto dinero habrá ahorrado al finalizar el año?

Enero, Febrero, Marzo, Abril, Mayo, Junio, Julio, Agosto, Sep., Oct., Nov., Diciembre.

 10€   11€      12€     13€      14€      15€     16€       17€        18€   19€    20€       21€

Un jardinero tiene que regar 20 árboles separados entre sí 2m y para regarlos cada vez va a un pozo a llenar el cubo que dista del primer árbol 4m.

1. ¿Cuántos metros anda para regar el primer árbol?
2. ¿Cuántos metros anda para regar el segundo árbol?¿Cuántos metros anda para regar el último árbol?
3. ¿Cuántos metros anda en total?

La primera semana del otoño recibo una paga de 10€. Como me porto bien cada semana me dan 1€ más. ¿Cuánto me dan en un año?

a₅₂=10+51·1=61

S₅₂=(10+61)·(52/2)=1846 euros

Cuánto suman los números múltiplos de 3 que están entre 7 y 98.

El primer número sería 9 y el último 96. El número de términos (96/3).2=30

S=(9+96)·(30/2)=105·15=1575

Fuentes:

Prof: F. López- D. Legal: M-007076/2009

Progresiones geométricas-Término general y Suma de términos

Son un apartado de las progresiones. Un término se calcula multiplicando el anterior por un número llamado razón.

Término general de la progresión geométrica

Una célula se divide cada segundo en dos, ¿Cuántas células hay a los 10 segundos y a los 20 segundos y a los 52 segundos?

Una célula se multiplica cada segundo en dos, ¿Cuántas células hay a los 8s y 40s?

Interpolar un término entre 18 y 162, que forme una progresión geométrica.

18·x es el número que buscamos, pero este multiplicado por x de nuevo tiene que dar 162.

Interpolar es poner entre ambos números.

18·x·x=162

x²=162/18=9

x=3

El número por tanto es 18·3=54

SUMA DE LOS TÉRMINOS DE UNA PROGRESIÓN GEOMÉTRICA

Si sumamos infinitos términos y la razón es un número comprendido entre 0 y 1, se queda la fórmula reducida a la siguiente:

1. Calcular la suma de los 5 primeros términos de una progresión de primer término 2 y razón 3.
2. Una bacteria se reproduce duplicándose  cada segundo. ¿Cuántas hay al minuto? ¿Y a la hora?
3. Un cliente de facebook le dice a 5 amigos un secreto y estos a su vez cada minuto a otros 5 distintos. ¿Cuántas personas lo saben a los 20 minutos?

Fuentes:

Prof: F. López- D. Legal: M-007076/2009