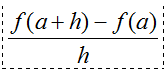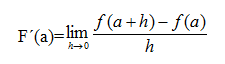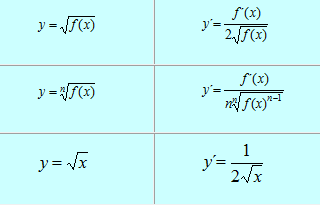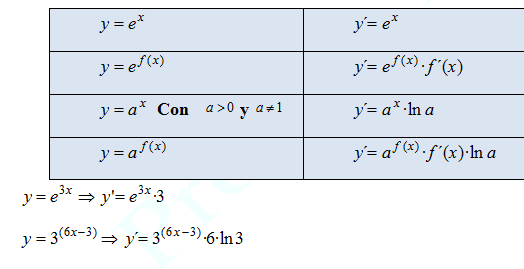Descartes, Newton y Leibniz favorecieron el desarrollo de la derivada, aunque el concepto del finito y el infinito lo trata Galileo al comparar los números y sus cuadrados.
DEFINICIÓN DE DERIVADA
La derivada es un concepto fundamental en cálculo y análisis matemático. Se refiere a la tasa de cambio instantánea de una función en un punto específico. En otras palabras, la derivada mide cómo cambia el valor de una función en respuesta a cambios infinitesimales en su variable independiente.
Es la pendiente de la recta tangente a la curva en un punto. La pendiente es la tangente del ángulo que forma la “recta tangente” con el eje de abscisas.
COCIENTE DE NEWTON O COCIENTE INCREMENTAL
Matemáticamente, la derivada de una función f(x) respecto a x, denotada comúnmente por f ‘(x) o dx/df, se define como el límite cuando la variable de cambio (ℎ) tiende a cero de la razón de cambio promedio en un intervalo pequeño:
Es el cociente entre lo que aumenta la función y lo que aumenta la variable.

Esta expresión representa la pendiente de la recta tangente a la curva de la función en el punto x.
La derivada proporciona información sobre la rapidez con la que la función está creciendo o disminuyendo en un punto dado.
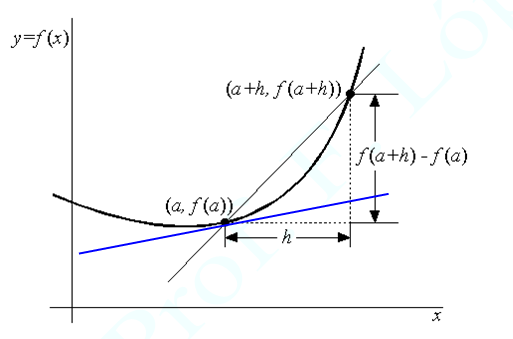
Se conoce como cociente de Newton o cociente incremental, pero también es la pendiente de la cuerda que pasa por A = (a, f(a)) y B= (a+h, f (a+h))
Si h tiende a cero el punto B se acerca al punto A y la recta cuerda se transforma en recta tangente, su pendiente es la derivada en un punto.
Se conoce como cociente diferencial o límite del cociente incremental.
Newton observó que una función curva no crece en la misma proporción que la variable. Compara el crecimiento de la curva con la pendiente de la cuerda en un cierto intervalo. A esto le conocemos actualmente como cociente incremental o cociente de Newton, también en economía tasa de variación.
Su método lleva fácilmente al cálculo de la pendiente de la recta tangente en un punto, pero por acuerdo entre Inglaterra y Alemania, esto se atribuye a Leibniz.
En 1665 introdujo el concepto de fluxión, que para él era la velocidad con la que una variable «fluye» (varía) con el tiempo.
Leibniz descubrió y comenzó a desarrollar el cálculo diferencial en 1675. Fue el primero en publicar los mismos resultados que Newton descubriera 10 años antes. En su investigación conservó un carácter geométrico y trató a la derivada como el límite de un cociente incremental y no como una velocidad. A él debemos el concepto de derivada o pendiente de la recta tangente a una curva en un punto.
Ejemplo
Supongamos que una pelota sigue la gráfica:

Como es un ejercicio que representa a un hecho real sería normal que solo se considere que x varía de x=0 a x=6.

Supongamos un intervalo:

Si resto 8-5=3 es lo que aumenta la variable, es decir f(x).
Si resto 2-1 es lo que aumenta la variable x.
Si divido los dos incrementos tengo lo que varía la función en ese intervalo
 que nos indicaría la velocidad media en el intervalo de tiempo que pasa de x=1 a x=2.
que nos indicaría la velocidad media en el intervalo de tiempo que pasa de x=1 a x=2.
Pero como la función es una curva ese crecimiento varía en cada punto y también la velocidad.
Entonces surge la derivada como el incremento puntual de la función que nos mide la velocidad en cada punto.

Esto indica que la velocidad que lleva si x=2 es 10metros/seg.
Si esto lo tenemos que hacer en cada punto sería muy complicado, entonces lo que debemos hacer es calcular la derivada en cada punto, es decir:
A esto le llamamos función derivada.
Las fórmulas de las derivadas se demuestran con la definición y permiten calcular las pendientes con más facilidad.
En este caso f´(x)=-2x+6 y si calculamos f´(2)=2, lo mismo de antes, pero ahora podemos sustituir cualquier punto y saber la velocidad en cada momento.
- Calcular la función derivada de F(x) = 1/x con la definición. Calcular la derivada en el punto x=2
Ahora lo hacemos con x=2

Si queremos hacer la derivada con esta fórmula para cada función en cada punto sería largo y complicado, por ello hemos demostrado en general las fórmulas de cada función y las aplicamos para obtener la función derivada.
Supongamos una función y = f (x). Si en el punto de la curva (a, f (a)) trazamos una recta tangente, la pendiente de dicha recta tangente es la derivada de la función en el punto. La derivada varía si varía el punto. La función derivada representa a todas las pendientes en todos los puntos
Cada función tiene una función derivada, se puede hallar con la definición o con la tabla de las fórmulas, que se demuestran con la definición.
- Demostrar la derivada de y= x²

Lo que demuestra que en un punto x=2 la pendiente de la recta tangente es f´(2)=2·2=4
Si tenemos que hacer la pendiente en cada punto debemos tener la función derivada, y para ello tenemos la tabla de fórmulas de cada función que permite derivar todo tipo de funciones.
DERIVADA DE LA FUNCIÓN POTENCIA
La función potencia siempre tiene la variable en la base y el exponente es un número.

El exponente pasa a multiplicar a la función, y la función queda elevada a un grado menos.

DERIVADA DE UNA CONSTANTE POR UNA FUNCIÓN

El exponente multiplica a la función, que ahora tiene un coeficiente que también queda multiplicado, y la función vuelve a quedar elevada el exponente menos.
DERIVADA DE UNA SUMA DE FUNCIONES
DERIVADA DE UNA CONSTANTE
![]() La derivada de una constante es cero.
La derivada de una constante es cero.
DERIVADA DE UN PRODUCTO DE FUNCIONES
DERIVADA DE UN COCIENTE

DERIVADA DE UNA RAÍZ

DERIVADA DE UNA FUNCIÓN LOGARÍTMICA
Siempre que en una derivada haya logaritmos, primero aplicamos sus propiedades y después derivamos, para simplificar la expresión.

Antes de derivar miro si se pueden aplicar las propiedades de los logaritmos, es más fácil y se simplifica mejor.

DERIVADA DE UNA FUNCIÓN EXPONENCIAL
DERIVADAS DE FUNCIONES TRIGONOMÉTRICAS


DEMOSTRACIÓN DE LA DERIVADA DEL ARCOSECANTE

DEMOSTRAR LA DERIVADA DEL ARCOCOSECANTE

DEMOSTRACIÓN DE LA DERIVADA DEL ARCOCOTANGENTE

DEMOSTRACIÓN DE LA DERIVADA DEL ARCOTANGENTE

DERIVADA DE UNA FUNCIÓN ELEVADA A OTRA FUNCIÓN

EJERCICIOS RESUELTOS DE DERIVADAS













EJERCICIOS DE DERIVADAS PARA REPASAR
Prof: F. López- D. Legal: M-007076/2009