septiembre | 2022 | MATEMÁTICAS CON MUCHO TRUCO

Para poder definir los vectores en el plano, debemos entender primero que es un plano y las coordenadas de sus puntos.

DEFINICIÓN DE PLANO

Un plano es el conjunto de pares de números reales.

Se representa por:

EJE HORIZONTAL «OX» ES EL EJE DE ABSCISAS
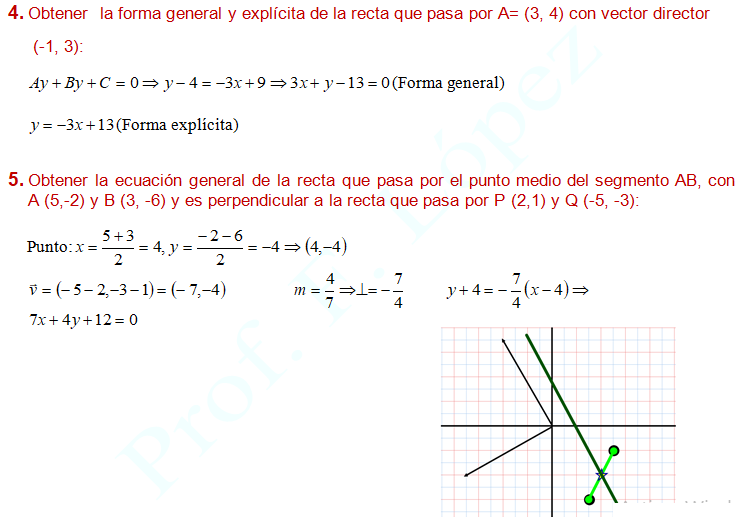
EJE VERTICAL «OY» ES EL EJE DE ORDENADAS

OPERACIONES CON LOS PARES DE PUNTOS

(a,b)+(c,d)=(a+c.b+d)
(a,b)-(c,d)=(a-c,b-d)
k(a,b)=(ka,kb)

DEFINICIÓN DE VECTOR

Un vector es un segmento orientado con origen en un punto A y extremo en B.

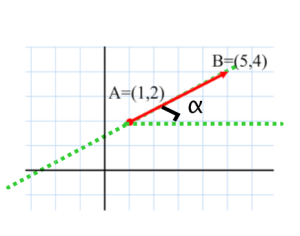
CARACTERÍSTICAS PRINCIPALES DE LOS VECTORES

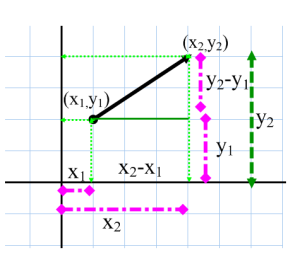
El módulo de un vector es la distancia entre el origen y el extremo. 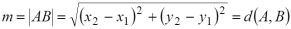.EL MÓDULO SE CALCULA POR EL TEOREMA DE PITÁGORAS.
La dirección queda determinada por la pendiente del vector. La pendiente es la tangente del ángulo que forma la recta que contiene el vector con el eje de abscisas, medido en sentido positivo.
⇒
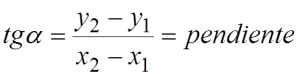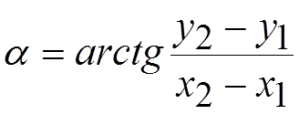
El sentido lo indica la flecha.

Los vectores opuestos entre sí tienen la misma dirección pero sentido contrario. El sentido es una flecha que se sitúa en al extremo del vector y que indica hacia donde se desplaza.

VECTORES EQUIPOLENTES

Son los que tienen el mismo módulo, dirección y sentido.

A todos ellos les representa el mismo vector en el origen.
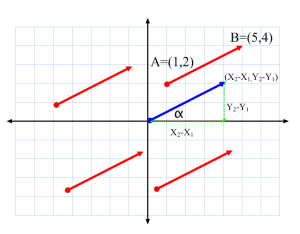
En el plano hay infinitos vectores que tienen el mismo módulo, dirección y sentido:

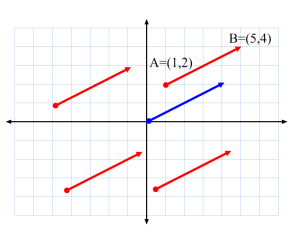
EL QUE ESTÁ EN AZUL ES EL EQUIPOLENTE EN EL ORIGEN DE TODOS LOS DEMÁS. ES EL REPRESENTANTE DE TODOS.
PAR CALCULAR SUS COORDENADAS, BASTA RESTAR EL EXTREMOS DEL ORIGEN DE CUALQUIERA DE ELLOS.
A=(x_1,y₁) Y B=(x₂, y₂)

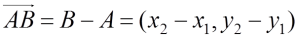
SUMA DE VECTORES

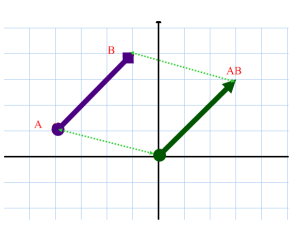
Para sumar dos vectores libres, se escogen como representantes dos vectores tales que el extremo final de uno coincida con el extremo origen del otro vector.

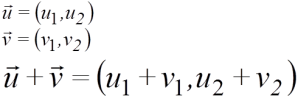
Si se toman como representantes dos vectores con el origen en común, se trazan rectas paralelas a los vectores obteniéndose un paralelogramo cuya diagonal coincide con la suma de los vectores.

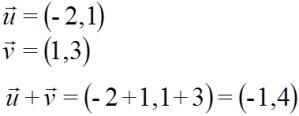
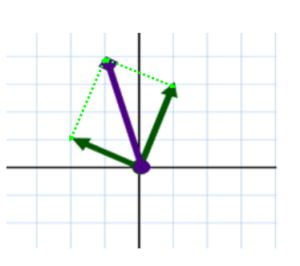
RESTAR ES SUMAR EL OPUESTO

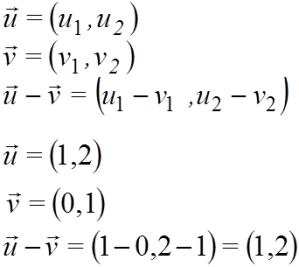
PRODUCTO DE UN NUMERO POR UN VECTOR

El producto de un número k por un vector da como resultado otro vector que tiene:

La misma dirección que el vector .
Del mismo sentido que el vector si k es positivo.
De sentido contrario del vector si k es negativo.
De módulo el /k/·/VECTOR/

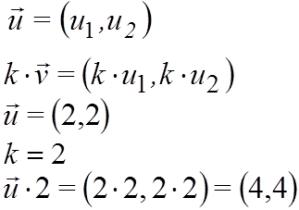
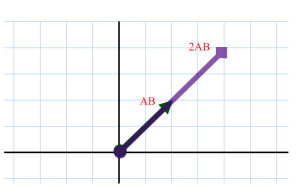
RECUERDA: SI MULTIPLICAMOS UN VECTOR POR UN NÚMERO SU DIRECIÓN NO VARÍA

COMBINACIÓN LINEAL DE VECTORES

Es un operación combinando las anteriores, , siendo a y b números.

Cualquier vector se puede poner como combinación lineal de otros dos que tengan distinta dirección.

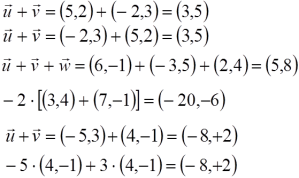
VECTORES LINEALMENTE INDEPENDIENTES

Dos vectores son linealmente independiente si al multiplicar cada vector por un número y el resultado es el vector cero, resulta que los escalares tienen que ser el número cero.

a·(1,1)+b·(-1,2)=(0,0)

Para probar si dos vectores son linealmente independientes, en el plano formamos con ellos un determinante Y TIENE QUE DAR DISTINTO DE CERO.

Lo vectores del plano L.I. no tienen la misma dirección.

(Un determinante es un conjunto de números ordenados en filas y columnas, de manera que el número de filas tiene que ser igual al número de columnas, y que se pueden resolver según el orden).

(No hay que confundir nunca un determinante con una matriz). La matriz va entre paréntesis y no se puede operar)

Dos vectores son linealmente independientes cuando su determinante da ≠0.

Si dos vectores son linealmente independientes, cualquier otro vector se puede poner en combinación de ellos.

PARA OPERAR COMBINACIONES LINEALES DE VECTORES, PODEMOS APLICAR CUALQUIER MÉTODO DE RESOLVER UN SISTEMA. SUSTITUCIÓN, IGUALACIÓN, CRAMER Y REDUCCIÓN O GAUSS.

EJEMPLO POR CRAMER

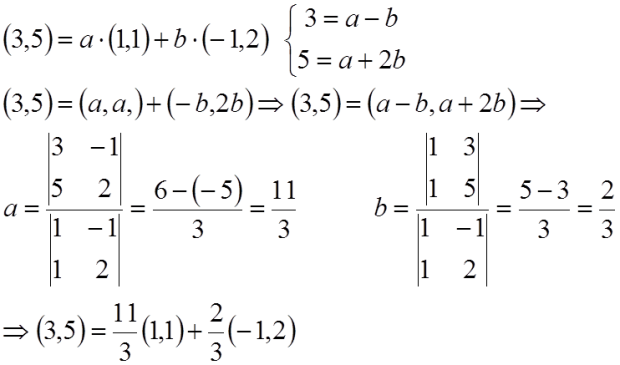
EJEMPLO POR GAUSS

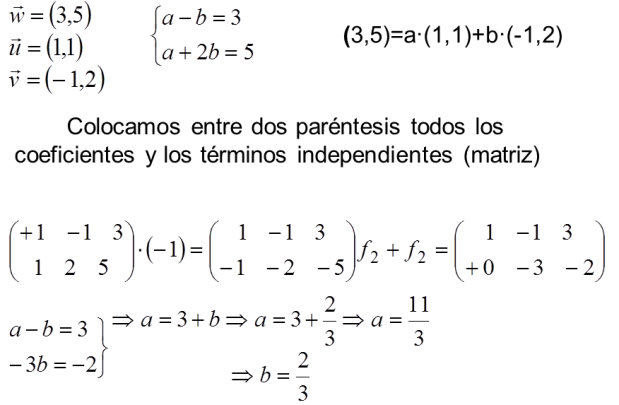
Prof: F. López- D. Legal: M-007076/2009

DEFINICIÓN DE ECUACIÓN DE LA RECTA EN EL PLANO

Es una expresión con dos variables que representa a todos los puntos de la recta y puede adoptar distintas formas, todas equivalentes entre sí.

Las dos variables, X e Y, se llaman: a la X variable independiente, la Y variable dependiente, porque es la que suelo despejar en función de la X.
Siempre que haga la ecuación de una recta, necesito un punto y la dirección de la recta, o dos puntos.

FORMAS DE LA ECUACIÓN DE LA RECTA

Son las distintas expresiones que representan a todos los puntos de la recta.

Son todas equivalentes.
DE UNAS DE PUEDE PASAR A OTRAS.

FORMA VECTORIAL

Si pasa por el origen, es simplemente multiplicar un vector por un número. Así represento a un conjunto de puntos alineados.
Si pasa por un punto P y es paralela al vector «v»

«λ» recibe el nombre de «PARÁMETRO» Y ES UN NÚMERO REAL CUALQUIERA.
SI NO FUESE REAL, SERIA PUNTOS SUELTOS ALINEADOS Y NO TODOS LOS PUNTOS DE UNA RECTA.

EJEMPLO: P=(2,3) y V=(3,1)

Para representarla, basta dar valores al parámetro «λ» y vamos obteniendo tantos puntos como queramos y siempre alineados.

FORMA PARAMÉTRICA

Consiste en despejar en la forma vectorial x e y.

Se puede obtener a partir de la forma vectorial.
Se puede hacer directamente, siempre que tengamos un punto por donde pasa y el vector.

⇒ Ejemplo

FORMA CONTINUA

Se trata de eliminar el parámetro de la ecuación.

Se puede construir directamente.
Se puede despejar a partir de la forma paramétrica.

Imagen7 ⇒ Ejemplo

FORMA PUNTO-PENDIENTE

Recibe ese nombre , porque queda en función del punto y de la pendiente del vector o de la recta.

⇒Ejemplo

Al coeficiente de x, es la pendiente de la recta y se representa por m.
La pendiente de una recta es igual a la tangente del ángulo que forma la recta o el vector con el eje de abscisas, medido en sentido contrario a las agujas del reloj y desde el eje OX positivo.

FORMA EXPLÍCITA O REDUCIDA

Se trata de dejar la forma con la variable «y» despejada.

Se puede despejar a partir de la forma punto pendiente o de la forma continua.
«m» es la pendiente de la recta.
«n» es la ordenada del punto de corte de la recta con el eje de ordenadas. (0,n)

1/3 es la pendiente
(0,7/3) el punto de corte de la recta con el eje «OY»
En la figura se muestra el vector de la recta, (3,1) y el vector perpendicular (1,-3) que se obtiene cambiando los números entre sí y uno de signo.

FORMA GENERAL

Se trata de dejar una ecuación, con dos variables e igualada a cero

. ⇒

Lo fundamental de la forma general es que es la manera idónea de tener una recta para resolver un sistema con otra y ver su punto de corte.
Otro punto importante es que los coeficientes de las variables forman un vector perpendicular a la recta.
(A, B) es un vector perpendicular a la recta, por tanto el vector de la recta es (B, -A).

FORMA SEGMENTARIA

Esta forma se obtiene a partir de la general.

SE TRATA DE DEJAR UNA EXPRESIÓN, DE TAL FORMA QUE LOS DENOMINADORES DE LAS VARIABLES , SON LAS MEDIDAS DE LOS SEGMENTOS DETERMINADOS POR LA RECTA AL CORTAR A LOS EJES DE COORDENADAS.